共计 6367 个字符,预计需要花费 16 分钟才能阅读完成。
龙年一开始,Sora 的横空出世令人瞩目,其声称自己是“全球顶尖的模拟视频生成模型”,引发了广泛关注。对此,有人悲观地预测,许多传统领域将面临颠覆,尤其是计算机图形学、短视频以及影视娱乐行业。随着 OpenAI 陆续公布更多技术细节,Sora 所生成的物理悖论视频在网络上引发热议。本文将结合现代数学,尤其是整体微分几何的视角,探讨 Sora 技术中的缺陷,希望能为 AI 研究及工程师们提供新的思路,促进技术进步。主要将运用流形嵌入理论、灾变理论、纤维丛示性类理论、热扩散方程以及最优传输方程的正则性理论进行分析。
流形分布定律
在深度学习领域,自然数据集被视为流形上的概率分布,这被称为 流形分布定律。我们将观察到的样本视为原始数据空间中的一个点,多个样本则形成一个稠密的点云,围绕着某个低维流形,这个流形即为数据流形。值得注意的是,点云在数据流形上的分布并不是均匀的,而是遵循特定的概率分布规律。
由此,我们不禁提出以下疑问:1. 为什么数据点云是低维的,而不是填满整个原始数据空间?2. 为什么点云的集合呈现为流形,即在局部是连续光滑的?
针对第一个疑问,我们可以解释为:自然现象遵循众多规律,这些规律的约束使得数据样本的维度降低,无法覆盖整个空间。例如,在分析自然人脸照片的数据集时,每个采样点对应一张图片,其维度为像素数量乘以三。尽管原始图像空间的每个点均为一幅图片,但仅有极少数符合人脸特征,故人脸流形无法填满整个原始图像空间。人脸的形成受限于诸多生理规律,例如左右对称性,显著减少了可用的像素数量。此外,由于五官等几何与纹理区域的相似性,这进一步降低了流形的维度。最终,控制人脸特征的基因数量极为有限,因此,人脸流形的维度远低于图像像素的总数。
同样,当我们观察平面区域的稳恒态温度分布时,根据热扩散定理,稳定的函数满足经典的 Laplace 方程,并由其边界条件唯一确定。如果我们在区域内部设置 n 个采样点,而边界上也有 n 个采样点,那么每个观察到的温度函数可以表示为维度为 n²的向量,即原始数据空间的维数为 n²,而实际流形的维数仅为边界函数的维数 n。因此,我们可以看到,满足物理定律的观测数据构成的数据流形,其维数通常远低于原始数据空间的维数。
对于第二个问题,可以这样理解:在大多数情况下,物理系统是适定的,但在临界状态下,物理系统会出现突变(可借助灾变理论描述)。物理定律通常通过偏微分方程系统来表达,微分方程的解由初值和边界值确定。适定性指的是,在能量守恒、质量守恒等物理限制下,初值与边界值的微小变化将导致解的逐渐变化。在偏微分方程的正则性理论中,这意味着边界的索伯列夫范数限制了解的索伯列夫范数等。当我们将解视为数据流形上的点,而边界视为其对应的局部坐标(即隐空间中的隐特征向量),从数据流形到隐空间的映射被称为编码映射,而从隐空间到数据流形的映射则为解码映射。正则性理论确保了编码与解码映射的连续性和光滑性,而解的唯一性则保证了这些映射是拓扑同胚或微分同胚。边界可以任意局部扰动,即隐变量存在一个开欧式圆盘邻域,这意味着符合特定物理定律的观测样本构成了数据流形。
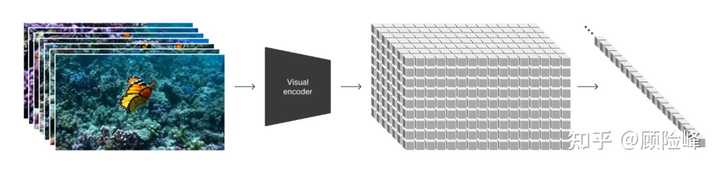
如图 1 所示,Sora 的训练集由短视频组成,每个样本为一个短视频,同类型短视频集合形成一个数据流形。Sora 将其编码至隐空间进行降维,随后在隐空间中将隐特征向量切割成补丁,并结合时间顺序形成时空补丁,即时空令牌。时空的概念在此至关重要,每个令牌都记录了短视频的帧序列号(时间)及当前帧的行列序号(空间)。
概率分布的转换
接下来,我们可以提出以下问题:3. 如何表示数据流形上的概率分布?
对于第三个问题,答案是:通过传输变换,将数据概率分布转换为计算机可以生成的高斯分布。该传输变换可以在原始数据空间或隐空间中进行。常见的传输变换包括最优传输变换和热扩散。我们可以借助流体力学的观点来进行解释。假设整个隐空间是一个水箱,内部充满了某种溶剂,其密度即为概率密度。我们对水箱进行扰动,使得液体流动,从而导致溶剂密度发生变化。我们将计算每个水分子的流向与流速,使得概率密度的熵不断增加,最终得到高斯分布。例如,考虑人脸数据分布,每个水分子即为一张人脸图片。我们不断为人脸图片添加噪声,生成一系列新图片,直至最终形成一张白噪声图片。这些图片的变化轨迹正如水分子的运动。最终,所有人脸图片转变为白噪声,而这些白噪声分布则符合高斯分布。这一过程被称为郎之万动力学。反过来,给定一张白噪声,我们可以沿着水分子轨迹追溯源头,获取一张人脸图片。这就是扩散生成模型的原理(diffusion model)。当然,也可以直接利用最优传输理论求解隐空间的同胚,将数据分布转化为高斯分布,这需要求解蒙日 - 安培方程。因此,数据分布的所有信息均由传输映射所包含,而传输映射则由深度网络实现。

如图 2 所示,Sora 在隐空间通过扩散过程(郎之万动力系统,逐渐为每个令牌添加噪声)将数据令牌的概率分布转化为高斯分布,并通过逆变换将隐空间中的白噪声令牌转换为隐数据令牌。
大语言模型的支持
Sora 结合了大语言模型 ChatGPT,显著提升了系统性能。首先,Sora 的训练样本由(文本,视频)对组成,部分视频的标题过于简短,字幕缺乏,因此 Sora 采用了 Dall- E 的重新标题技术。
其训练集包含了一些高质量样本(高度描述性的字幕与短视频),由此构建了短视频数据流形(包括时空令牌流形)。每个流形用其字幕(标题)标识。对于缺乏标题或字幕含糊的劣质短视频,Sora 将其编码至隐空间,并在隐空间中寻找相近优质视频的隐特征向量,然后将优质视频的字幕(标题)拷贝给劣质视频。借助这种方法,Sora 为所有训练视频数据添加了高度描述性的字幕,从而提升了训练集质量并进一步增强了系统性能。
同时,大语言模型能够对用户输入的提示进行扩展,使其更为精准与描述性,从而让生成的视频更符合用户需求,使得 Sora 如虎添翼。然而,Sora 依然存在不少缺陷,以下通过实例进行分析。
相关性与因果律的冲突
ChatGPT 将语句拆解为令牌,然后利用 Transformer 学习上下文中令牌间的连接概率分布。类似地,Sora 也将视频分解为时空令牌,学习上下文中令牌间的连接概率,并依据这一概率分布由白噪声生成令牌,连接令牌并解码为短视频。每个令牌代表图像或视频中的局部区域,不同局部区域之间的拼接就成为关键问题。Sora 相对独立地学习每个令牌,利用训练集中体现的概率来表达令牌间的空间关系,因此难以精准表达令牌间时空的因果关系。
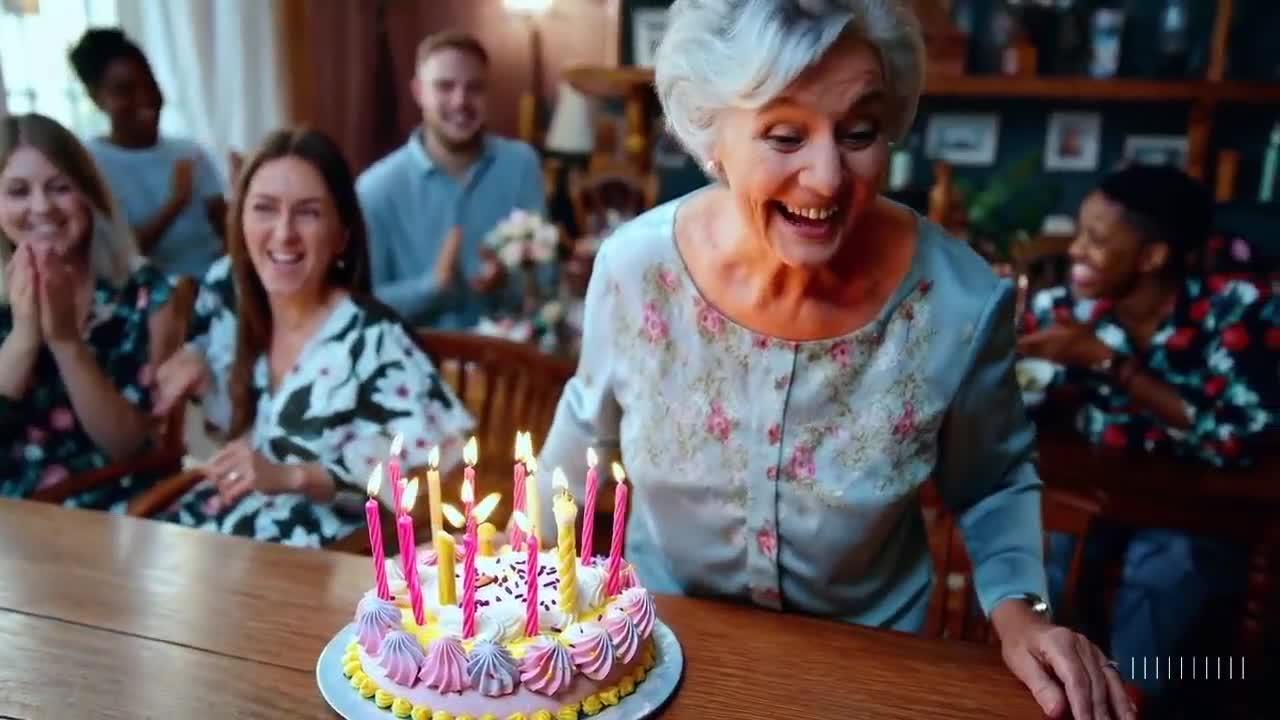
如视频 1 所示,Sora 生成的视频中,每一帧都显得极为真实,但当老奶奶吹熄生日蜡烛时,蜡烛的火焰却纹丝不动。若我们将视角缩小到每个令牌的区域,可以看到精美的画面,令牌之间的衔接也非常自然,但当相隔较远的令牌间存在因果联系时,例如吹出的气流对火焰的影响,两个令牌之间的物理因果关系并未体现。这表明,Transformer 所表达的令牌间的统计相关性,无法精准反映物理因果律。尽管 Transformer 在一定程度上可以处理自然语言,但自然语言无法准确表述物理定律,而物理定律的精确表达则需依赖偏微分方程。这反映了基于概率的世界模型的某种局限性。
局部合理与整体荒谬的矛盾
当前 Sora 在相邻令牌间的拼接相当合理,但整体拼接的视频却可能出现各种悖论。这说明局部拼接与整体拓展之间存在鸿沟。

在观察“幽灵椅子”视频时,如果将视角集中在屏幕中央的某个局部区域,视频显得非常合理。经过仔细检测,不同令牌间的连接也非常连续光滑。然而,整个椅子却悬空如鬼魅,这与日常经验相悖。这种“局部合理,整体荒谬”的生成视频,表明 Transformer 仅学会了令牌间局部的连接概率,却缺乏时空上下文的整体观念。整体观念在此来自物理中的重力场,尽管局部并未显示,但整体始终存在。

例如,Sora 生成的“四足蚂蚁”视频中,蚂蚁的动作栩栩如生,宛如行云流水。局部上非常流畅自然,令人联想到或许在某个星球上确实存在这种四足蚂蚁。然而,整体而言,地球的自然界并没有四足蚂蚁。这里局部的合理性无法保证整体的合理性,这里的全局观念源于生物学的事实。

再如,Sora 生成的“南辕北辙跑步机”视频,若我们观察每一个局部区域,看到的视频都是合理的,视频令牌间的连接也很自然,但整体视频却显得荒谬,跑步机与跑步者的方向相反。这个视频的全局观与人体工程学的事实相悖。
这些实例表明,当前 Transformer 虽然能够学习局部上下文,却无法学习更为全局的上下文,而这个全局可能涉及物理中的重力场、生物学中的物种分类等。正是朱松纯教授提出的 AI 世界中的暗物质思想。尽管每个训练样本隐含地表达了全局观念,但令牌化的过程中割裂了全局观,有限地保留了临近令牌间的连接概率,导致局部合理而整体荒谬的结果。
现代整体微分几何重视整体与局部的矛盾,为此发明了多种理论工具。例如,我们可以在拓扑流形的局部构造光滑标架场,但无法全局推广,障碍在于纤维丛的示性类。在复流形上,我们可以构造亚纯函数,但整体上无法将局部函数拼接成整体的亚纯函数,这种局部向整体的差异可通过层的上同调理论精确描述。许多物理理论都可表示为特定纤维丛的示性类理论,例如拓扑绝缘体理论。这种局部容易构造而整体推广困难的数学理论,正是人类探索自然的智慧结晶。目前,这种整体的拓扑、几何观点尚未应用于 AI 领域。如果 Transformer 能够自动学习到上下文中的整体障碍,AI 将更高效地探索自然界。
临界状态的缺失
自然界中的绝大多数物理过程均为稳恒态与临界态的交替。在稳恒态中,系统参数缓慢变化,观察数据容易获取;而在临界态(灾变状态)中,系统突变,令人措手不及,难以捕捉观察数据。因此,临界态的数据样本极为稀少,几乎在训练集中为零测度。因此,Sora 系统所学习到的数据流形大多由稳恒态样本构成。物理过程中的临界态样本多分布在数据流形的边界。因此,在生成过程中,Sora 容易生成稳恒态的视频片段,但往往跳过临界态。然而在人类认知中,最为关键的观察恰恰是概率几乎为零的临界态。

在 Sora 生成的果汁泼溅视频中,存在两个稳恒状态:水杯直立的状态和果汁已泼溅的状态,但关键的临界状态:果汁从杯中流洒出来的过程却没有生成。尽管仅仅是短暂的几帧,但对于人类感知整个过程至关重要。Sora 未能生成关键临界态图像的原因可能如下:
物理过程中不同稳恒态样本生成的数据流形的不同连通分支,临界态样本通常位于稳恒态流形的边界附近,处于两个稳恒态流形的边界之间。热力学扩散过程使流形的边界变得模糊,从而混淆了流形的界限,生成的过程显得含糊不清。换言之,临近状态对应于数据流形的边界,学习过程中应保持边界情形,而非产生模式混淆。
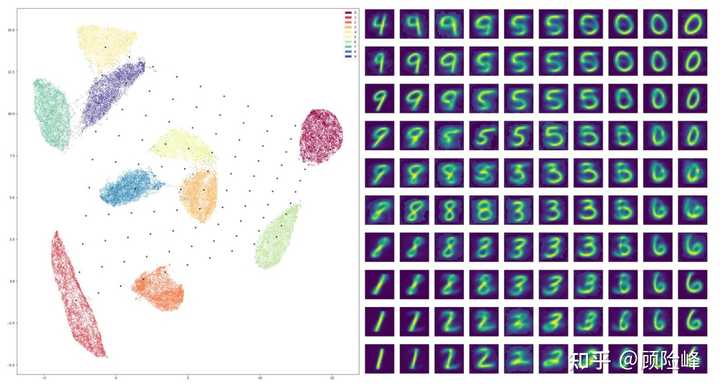
如图 3 所示,我们用 MNIST 训练了一个编码解码器,绘制了数据集的隐空间分布,十个手写数字对应十个团簇,每个团簇是一个模式,即数据流形的一个连通分支。团簇的边界则是数据隐空间分布支集的边界。我们在隐空间生成了 100 个采样点,通过解码生成 100 个手写数字图像。如果采样点落在某个团簇内部,则生成的图像清晰;如果落在团簇边界外,则生成的图像模糊,往往是两个手写数字的融合。因此,识别数据流形的边界对识别临界状态至关重要。
Sora 所采用的热门扩散模型在计算传输映射时,必然会光滑化数据流形的边界,从而混淆不同模式,导致错过临界态图像的生成。因此,视频看似从一个状态突然跳跃到另一个状态,而缺少了关键的倾倒过程,从而导致物理上的荒谬。

在视频 6 中,我们展示了另一种因跨越流形边界而出错的情形。Sora 生成的小狗群在嬉戏打闹,时而遮挡,时而散开。在某一瞬间,屏幕中的三只小狗突然变为四只小狗。我们可以解释为:四只小狗的图像构成一个流形(或连通分支),三只小狗的图像构成另一个分支,而在四只小狗图像的流形边界处,发生了临界事件:四只小狗彼此遮挡,图片中只能看到三只小狗。Sora 的扩散模型未能识别流形的边界,冲破了这一界限,导致在三只小狗和四只小狗的图像流形间跨越。正确的做法应是先识别流形的边界,然后在物理无法跨越的情况下(如三只与四只小狗),在边界处折回原来的流形。
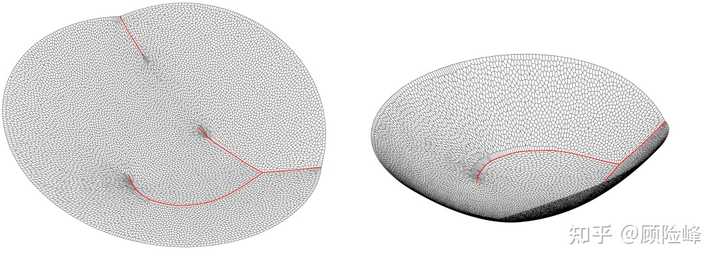
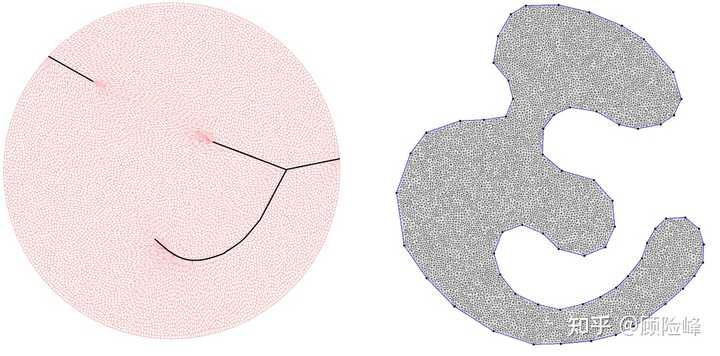
扩散模型的缺陷可以通过基于几何方法的最优传输模型克服。如图 4 所示,假设我们计算从圆盘内部均匀分布到右侧海马形状区域内的均匀分布的最优传输映射,根据相应的 Brenier 定理,该映射由某个凸势能函数的梯度映射给出。这一势能函数满足蒙日 - 安培方程,其连续、非可导的集合投影到圆盘区域的奇异集合(黑色曲线),规则点映射到目标区域的规则点,而奇异集合映射到目标区域的边界(每个奇异点同时映射到左右两个边界点)。当我们跨越奇异集合时,意味着跨越了两个稳恒态,必然发生临界(灾变)事件,即物理事件的稳恒态被打破。由此可见,精准识别传输映射的奇异集合、探测临界(灾变)状态,对于物理世界建模至关重要。
总结
综上所述,尽管 Sora 声称是“全球顶尖的视频生成模型”,但其当前的技术路线并未能准确模拟世界的物理规律。首先,利用概率统计所表达的相关性无法精确反映物理定律的因果性,自然语言的上下文相关性无法与偏微分方程的精密度相提并论;其次,Transformer 能够学习临近时空令牌间的连接概率,却无法评判全局的合理性,整体的合理性需要更高层次的数学理论视角或更深厚的自然与人文科学背景,当前的 Transformer 尚未领悟这些全局观念;此外,Sora 忽视了物理过程中至关重要的临界(灾变)态,既因临界态样本稀缺,也因扩散模型模糊了稳恒态数据流形的边界,导致生成的视频在不同稳恒态之间跳跃。基于几何方法的最优传输理论框架,能够精准捕捉稳恒态数据流形的边界,从而强调临界态事件的生成,避免不同稳恒态之间的跨越,更加接近物理的真实。
目前,以 Sora 为代表的数据驱动世界模拟模型与以第一性原理构建的物理定律和偏微分方程的世界模拟模型正在展开激烈竞争。这或许标志着人类历史的重大转折点。希望年轻的读者能够积极投身于这一时代潮流,运用自身的智慧推动科技与社会的发展!